EnergySystems
This model package has been specially designed for solving optimal design and control problems using dynamic optimization in Modelon Impact. To formulate and solve the optimization problem, the end-user needs to provide the following information:
- Initial guess for the optimization
- Optimization objective
- Time horizon of the optimization (time period)
Either or both of the following:
- Degrees of freedom varying in time
- Degrees of freedom constant in time (parameters)
Optionally,
- Inequality constraints
- Boundary conditions
Some specific blocks and conventions have been derived to let the user conveniently enter all this information.
Dynamic Optimization
Modelon Impact allows you to solve dynamic optimization problems on nonlinear, dynamic, physical Modelica models using the "Dynamic Optimization" custom function included in this library, which can be accessed by hovering over the "Simulate Button" and selecting the corresponding option.
For selected Demos and Experiments in this library, Modelon Impact will optimize the degrees of freedom (DOFs) of the System Model. DOFs can be parameters or control inputs of the system.
Solving and setting up such an optimization problem can be a difficult task.
This custom function will simplify the workflow by automatically parsing and transferring the problem, as well as performing the necessary preparations ("Initial Guess") before performing the actual optimization. The problem is then solved using a nonlinear solver, like IPOPT, which solves the problem iteratively, starting from the initial guess. The initial guess is derived using a dynamic simulation where the initial guess signals for optimizable inputs are computed e.g. using some simple feedback controller.
All optimizable ESL experiments should extend from EconomyOptimizationTemplate which introduces the top level Boolean parameter 'initialSimulationPhase'. Based on that parameter, conditional components can be introduced that are only relevant for the initial dynamic simulation and the optimization, respectively.
For instance, the figure below shows graphical overview of the experiment .EnergySystems.Examples.EconomicDispatch in which the green frame bounds the components included in the optimization problem. This frame is not a connection and serves as graphical annotation only. Models included within the frame should be at least twice differentiable. See the .EnergySystems.Examples package for other best practice examples.
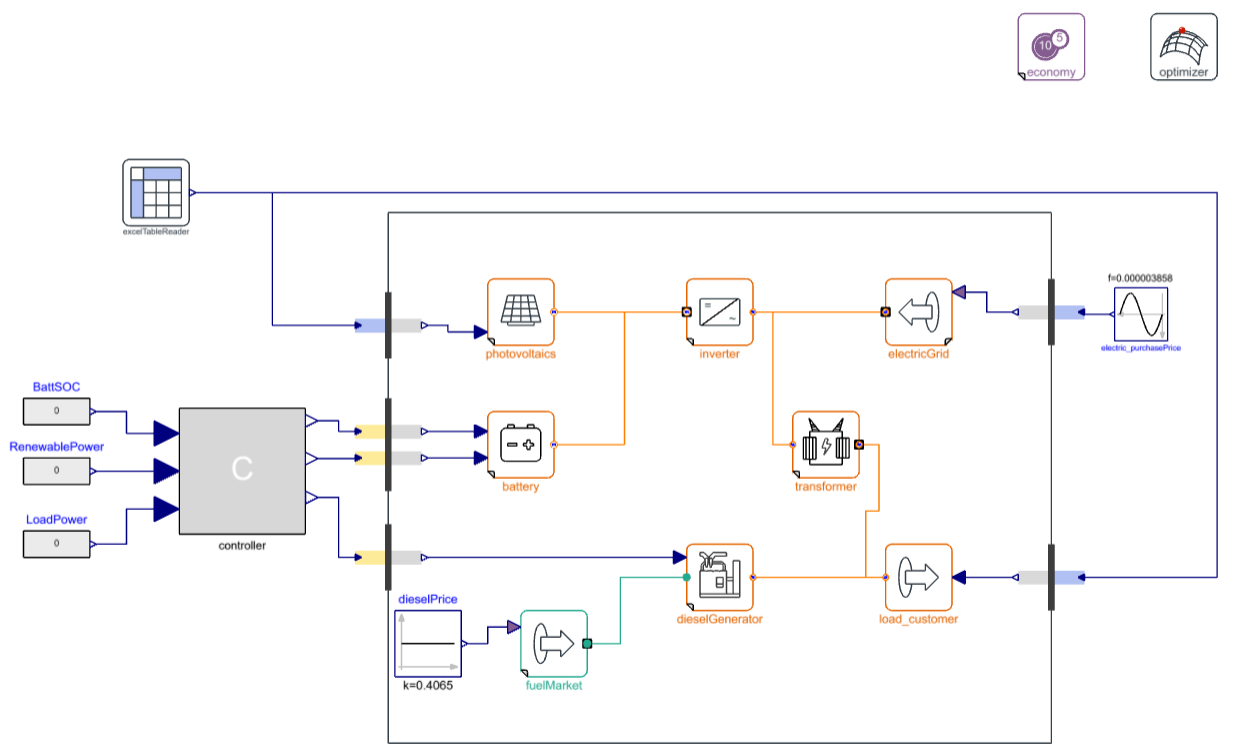
Initial guess for the optimization (Dynamic Simulation)
In order to generate start values for the optimization process, the model needs to be able to run successfully for the duration of the optimization time horizon. For that purpose, simple control strategies may be necessary. Ideally, such a control strategy generates a "feasible" result, i.e. the constraints are not being violated.
This ensures that there exists a feasible solution which should improve robustness of the algorithm.
Controller components needed for the initial guess simulation need to be "conditionally removed". Please refer to the Modelon Help Center's Best Practice guide on dynamic optimization.
Optimization objective
The objective to be minimized/maximized is defined in the optimizer block and the optimization model is expected to contain a top-level instance of this block named "optimizer", which is automatically included when using the aforementioned template.
The objective function can have two terms (either or both):
- MayerObjective: a term where the final value (i.e. at final time of optimization time horizon) will be optimized
- ObjectiveIntegrand: this term will be integrated over the time horizon.
Please refer to the options in the optimizer block.
Degrees of freedom varying in time
If a model input is a degree of freedom (optimal control), connect it to the output of a .EnergySystems.ScenarioSetup.OptimalControl block. This block needs an initial guess, which must be provided at its input.
The components creating the signals for the initial guess are not needed during the optimization phase and should therefore be conditionally removed based on the top level Boolean parameter 'initialSimulationPhase. Please refer to the code layer and see how this is achieved in the declaration of the controller units of the examples.
Degrees of freedom constant in time
Some models contain parameters that can be optimized. These parameters have been paired with Boolean parameters whose names end with the suffix "_free_" which could be found under the model Optimization tab. E.g. many models in our library contain an optimizable scaling factor "scalingFactor" which will be optimized when using the "Dynamic Optimization" custom function and setting the parameter scalingFactor_free_ to true. This will result in the components output/capacity to be multiplied by that factor. For example, in the case of a battery model, setting battery.scalingFactor_free_ to true means that the optimal capacity with respect to the objective function, the constraints and boundary conditions can be found.
.EnergySystems.ScenarioSetup.OptimalParameter is a convenience class which allows user to optimize other parameters as well. Drag the model into the top level of your system model and reference its parameter value to the component parameter you want to optimize.
Boundary conditions
Time varying boundary conditions (inputs) can be defined in external files and imported into the Modelica model. In the simulation/initialization model, blocks like .EnergySystems.ScenarioSetup.ExcelTableReader can be used to import the time-varying boundary conditions. To avoid unnecessary complexity in the optimization model, the input boundary conditions are imported from the initial simulation. To make this process simple, we use the .EnergySystems.ScenarioSetup.BoundaryCondition block, which will "record" the time series and transfer it to the optimization problem. Insert this block between your table data and the model which must be provided by this input. To remove the table data conditionally while optimizing, instantiate it based on the top level Boolean parameter 'initialSimulationPhase.
Constraints
Normal min and max attributes in the Modelica code will be considered as hard inequality constraint in the optimization. However, variables containing the constraint may be eliminated to improve performance. A specific block, .EnergySystems.ScenarioSetup.Constraint has been created to conveniently specify constraints which will NOT be eliminated during optimization.